Intro to Robotics Programming: Part 3

Posted: March 23, 2016

Hello Robot 2: The Return of Rob

We left Rob in an odd state last time. The poor little guy could go up and down, left and right, but never turn! We don't drive down the street or even walk that way. But wait, isn't this a 2D world? What happened to just $x$ and $y$ ? Rob's state, and indeed the state of all objects, must include more information to fully describe its pose in the world. So we must introduce a third parameter $\theta$ (theta) to describe Rob's orientation (in this case, as is standard, relative to the positive $x$ -axis, and positive in the "counter-clockwise" direction).

$[x, y, \theta]$ now fully describes our robot in some chosen coordinate system. This complete description is known as the configuration space of our robot.

Updated Movement

What's the importance of $\theta$ to our simple robot? Well, most robots don't strafe, because they are on wheels (unless you've got those slick Mecanum wheels). Let's pretend Rob is the same, and can only move forward and backwards, and turn clockwise and counter-clockwise. This is how differential drive (diff-drive) robots work. With two wheels and an unpowered caster, you turn by moving both wheels in opposite directions. Vary the difference in the (opposite) speeds, and you get different curved paths.

Let's give Rob a $\theta$ by replacing our previous process_user_input function:

from math import pi

# ...

def process_user_input(dt):
    angular_vel = 0.2 * 2 * pi  # rotations/sec -> radians/sec
    angular_delta = angular_vel * dt

    if keyboard[key.RIGHT]:
        rob_body.angle -= angular_delta
    if keyboard[key.LEFT]:
        rob_body.angle += angular_delta

We've taken advantage of pymunk's build-in Body.angle property to hold our $\theta$ . We then convert a human-sensible "rotations per second" into radians, and calculate our discrete delta.

Now, what about direction? If we leave the rest of the function as it was, Rob will only be able to travel up and down! We need to use $\theta$ as Rob's heading, and calculate his displacement from there.

from math import pi

# ...

def process_user_input(dt):
    angular_vel = 0.2 * 2 * pi  # rotations/sec -> radians/sec
    angular_delta = angular_vel * dt

    linear_speed = 0.6  # m/s
    distance = linear_speed * dt * M_TO_PIXELS  # m/s * s -> pixels
    heading = unit_direction_vector(rob_body.angle)
    displacement = tuple([distance * x for x in heading])

    if keyboard[key.RIGHT]:
        rob_body.angle -= angular_delta
    if keyboard[key.LEFT]:
        rob_body.angle += angular_delta
    if keyboard[key.UP]:
        rob_body.position += displacement
    if keyboard[key.DOWN]:
        rob_body.position -= displacement

The scalar distance calculation is the same, but now we have a displacement that depends on $\theta$ . But wait, what's this unit_direction_vector function? Brace yourself, we're diving into our first math of the series...

Note: I've chosen to do the linear displacement calculation with the previous time-step's $\theta$ . I don't know a good reason to do this one way or the other, so I picked one, and it looks good enough.

Of Robots and Triangles

As you may remember from high school, the trigonometric functions $\cos$ and $\sin$ relate angles with side lengths. Specifically, if we have the triangle:

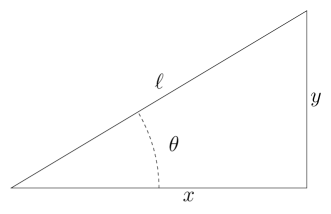
right triangle

We know that:

$\cos(\theta) = \frac{x}{\ell} \\ \sin(\theta) = \frac{y}{\ell} \\$

Remember, we have a $\theta$ and we're trying to solve for the $x$ and $y$ components of our vector. So "solving" the equations we get:

$x = \ell \cos(\theta) \\ y = \ell \sin(\theta) \\$

What is $\ell$ ? That is our scale factor, or the magnitude of the vector. If we set $\ell = 1$ , we have a unit vector that gives us the pure directional components that represent our angle. Our definition of unit_direction_vector then becomes:

from math import cos, sin

def unit_direction_vector(theta=0.0):
    return cos(theta), sin(theta)

And we scale it appropriately based on our set speed and dt.

This directional distance covered is known as displacement. Like speed and velocity, distance is a scalar value, and displacement is a vector, meaning both magnitude and direction. Since we simulate over discrete time-steps, these small displacements determine the resolution of our motion simulation. That will be important when we talk about collision detection.

Wrapping Up

Rob now has fairly realistic motion primitives, and we can joystick him around like an RC car. However, wheels and a human operator do not a robot make. In the next article, we'll look at how to take a higher level command (namely a point in space), and have the robot figure out how to get there himself.

The complete code for this article can be found in https://github.com/ClintLiddick/robotics_intro/blob/master/roboticsintro/hellorobot/rotation.py.

Next article: part 4